$$$$

Troubles with the Infinite

Real analysis is born out of our desire to understand infinite processes, and to overcome the difficulties raised by taking infinity seriously in this way. To appreciate this, we begin with an overview of some famous results from antiquity, as well as several paradoxes that arise from taking them seriously, if we are not careful.

The Diagonal of a Square

Around 3700 years ago, a babylonian student was assigned a homework problem, and their work (in clay) fortuitously survived until the modern day.

Tablet YBC-7289

The problem involved measuring the length of the diagonal of a square of side length $1/2$, which involves the square root of 2. The tablet records a babylonian approximation to $\sqrt{2}$ (Though it does so in base 60, where the ‘decimal’ expression is $1.(24)(51)(10)$) $$\sqrt{2}\approx \frac{577}{408}\approx 1.414215686\cdots$$

Definition 1 (Base Systems for Numerals) If $b>1$ is a positive integer, base-b refers to expressing a number in terms of powers of $b$. In base 10 we write $432$ to mean $4\cdot {10}^2+3\cdot {10}^1+2\cdot {10}^0$, whereas in base $5$ the string of digits $432$ would denote $4\cdot 5^2+3\cdot 5^1+2\cdot 5^0$.

Numbers between $0$ and $1$ can also be expressed in a base system, using negative powers of the base. In base $10$, $0.231$ means $2\cdot {10}^{-1}+3\cdot {10}^{-2}+1\cdot {10}^{-3}$, whereas in base $5$ the same string of digits would denote $2\cdot {10}^{-1}+3\cdot 5^{-2}+1\cdot 5^{-3}$.

The babylonians used base $60$, meaning all numbers were written as a series in ${60}^n$ for $n$ ranging over the integers. This tablet records the approximate square root of $2$ as

$$1.(24)(51)(10)$$

Which, in base 60 denotes

$$\begin{array}{rl}\sqrt{2}& \approx 1\cdot {60}^0+24\cdot {60}^{-1}+51\cdot {60}^{-2}+10\cdot {60}^{-3}\\ & =1+\frac{24}{60}+\frac{51}{{60}^2}+\frac{10}{{60}^3}\\ & =1+\frac{24}{60}+\frac{17}{1200}+\frac{1}{21600}\\ & =\frac{577}{408}\end{array}$$

Exercise 1 By inscribing a regular hexagon in a circle, the Babylonians approximated $\pi$ to be $25/8$. Compute the base 60 ‘decimal’ form of this number.

The tablet itself does not record how the babylonians came up with so accurate an approximation, but we have been able to reconstruct their reasoning in modern times

Example 1 (Babylonian Algorithm Computing $\sqrt{2}$) Starting with a rectangle of area $2$, call one of its sides $x$. If the rectangle is a square, then $x=\sqrt{2}$ exactly. And the closer our rectangle is to a square, the closer $x$ is to $\sqrt{2}$. Thus, starting from this rectangle, we can build an even better approximation by making it more square. Precisely, the side lengths of this rectangle are $x$ and $2/x$, and a rectangle with one side the average of these two numbers, will be closer to a square than this one.

Starting from a rectangle with side lengths 1 and 2, applying this procedure once improves our estimate from $1$ to $3/2$, and then applying it again improves it to $577/408$. This Babylonian approximation is just the third element in an infinite sequence of approximations to $\sqrt{2}$

Exercise 2 (Babylonian Algorithm Computing $\sqrt{2}$) Carry out this process, and show you get $577/408$ as the third approximation to $\sqrt{2}$. What’s the next term in the sequence? How many decimal places is this accurate to in base 10? (Feel free to use a calculator of course!)

Exercise 3 (Computing Cube Roots) Can you modify the babylonians procedure which found approximates of $\sqrt{2}$ to instead find rational approximates of $\sqrt[3]{2}$?

Here, instead of starting with a rectangle of sides $x,y$ let’s start with a three dimensional brick with a square base (sides $x$ and $x$), height $y$, and area $2$. Our goal is to find a “closer to cube” shaped brick than this one, and then to iterate. Propose a method of getting “closer to cube-shaped” and carry it out: what are the side lengths of the next shape in terms of $x$ and $y$?

Start with a simple rectangular prism of volume $2$ and iterate this procedure a couple times to get an approximate value of $\sqrt[3]{2}$. How close is your approximation?

It is clear from other Babylonian writings that they knew this was merely an approximation, but it took over a thousand years before we had more clarity on the nature of $\sqrt{2}$ itself.

Pythagoras

We often remember the Pythagoreans for the theorem bearing their name. But while they did prove this, the result (likely without proof) was known for millennia before them. The truly new, and shocking contribution to mathematics was the discovery that there must be numbers beyond the rationals, if we wish to do geometry.

Theorem 1 ($\sqrt{2}$ is irrational) There is no fraction $p/q$ which squares to $2$.

To give a proof of this fact we need one elementary result of number theory, known as Euclid’s Lemma (which says that if a prime $p$ divides a product $ab$, then $p$ must divide either $a$ or $b$).

Proof. (Sketch) Assume $p/q$ is in lowest terms, and squares to 2. Then $p^2/q^2=2$ so $p^2=2q^2$. Thus $2$ divides $p^2$, so in fact 2 divides $p$ (Euclid’s lemma), meaning $p$ is even.

Thus, we can write $p=2k$ for some other integer $k$, which gives $(2k{)}^2=2q^2$, or $4k^2=2q^2$. Dividing out one factor of 2 yields $2k^2=q^2$< so $2$ divides $q^2$, and thus (Euclid’s lemma, again) $2$ divides $q$.

But now we’ve found that both $p$ and $q$ are divisible by $2$, which means $p/q$ is not in lowest terms after all, a contradiction! Thus there can not have been any fraction squaring to 2 in the first place.

Exercise 4 Following analogous logic, prove that $\sqrt{3}$ is irrational. Generalize this to prove that $\sqrt{6}$ is irrational. But be careful! Make sure that your proof doesn’t also apply to $\sqrt{9}$ (which of course, IS rational).

Knowing now that $\sqrt{2}$ is irrational, it is clear that the Babylonian procedure will never exactly return the correct answer, as if it starts with a rationally-sided rectangle, it’ll always produce another with rational side lengths. But its a natural question to wonder just how good are the babylonian approximations?s

Definition 2 (The Babylonian Algorithm and Number Theory) Because $\sqrt{2}$ is irrational, there is no pair of integers $p,q$ with $p^2=2q^2$. Good rational approximations to $\sqrt{2}$ will almost satisfy this equation, and we will call an approximation excellent if it is only off by $1$: that is $p/q$ is an excellent approximation if $$p^2=2q^2+1$$

Exercise 5 (The Babylonian Algorithm and Number Theory) Prove that all approximations produced by the babylonian sequence starting from the rectangle with sides $1$ and $2$ are excellent, by induction.

To acomodate this discovery, the Greeks had to add a new number to their number system - in fact, after really absorbing the argument, they needed to add many. Things like $\sqrt{3}$, but also $$\sqrt{1+\sqrt{3-\sqrt{2+\frac{\sqrt{3}+\sqrt{2}}{5}}}}$$ are called constructible numbers, as they were constructed by the greeks using a compass and straightedge, to extend the rational numbers.

Quadrature of the Parabola

The idea to compute some seemingly unreachable quantity by a succession of better and better approximations may have begun in babylon, but truly blossomed in the hands of Archimedes.

In his book The Quadrature of the Parabola, Archimedes relates the area of a parabolic segment to the area of the largest triangle that can be inscribed within.

Theorem 2 The area of the segment bounded by a parabola and a chord is $4/3^{rd}$s the area of the largest inscribed triangle.

A parabolic region and its largest inscribed triangle

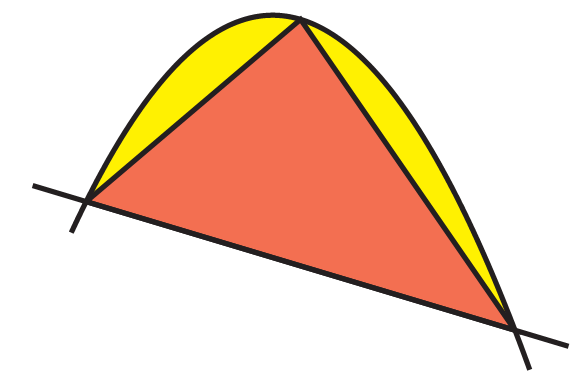
After first describing how to find the largest inscribed triangle (using a calculation of the tangent lines to a parabola), Archimedes notes that this triangle divides the remaining region into two more parabolic regions. And, he could fill these with their largest triangles as well!

These two triangles then divide the remaining region of the parabola into four new parabolic regions, each of which has their own largest triangle, and so on.

Archimedes’ infinite construction of the parabolic segment from triangles

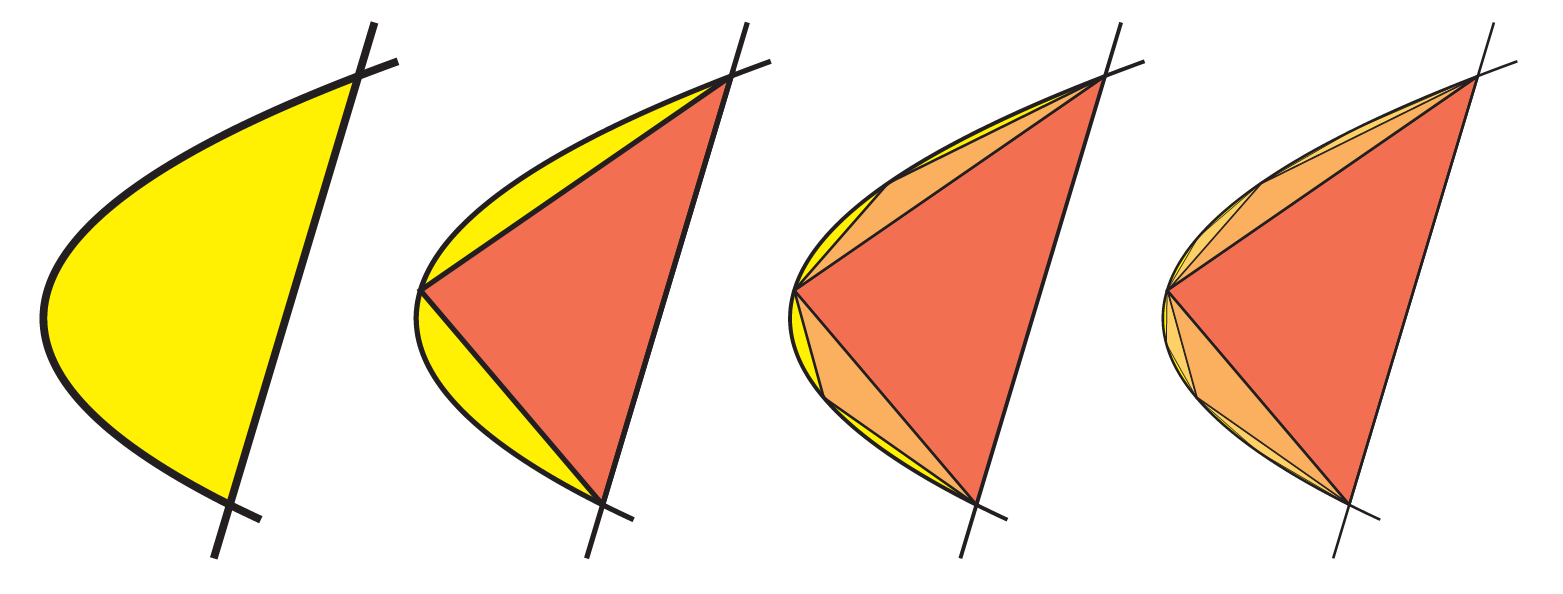
Archimedes proves that in the limit, after doing this infinitely many times, the triangles completely fill the parabolic segment, with zero area left over. Thus, the only task remaining is to add up the area of these infinitely many triangles. And here, he discoveries an interesting pattern.

We will call the first triangle in the construction stage 0 of the process. Then the two triangles we make next comprise stage 1, the ensuing four triangles stage 2, and the next eight stage 3.

Proposition 1 (Area of the $n^{th}$ stage) The total area of the triangles in each stage is $1/4$ the total area of triangles in the previous stage.

If $A_n$ is the area in the $n^{th}$ stage, Archimedes is saying that $A_{n+1}=\frac{1}{4}{A}_n$. Thus

$$A_0=T{A}_1=\frac{1}{4}T{A}_2=\frac{1}{16}T{A}_3=\frac{1}{64}T\dots$$

And the total area $A$ is the infinite sum

$$\begin{array}{rl}A& =T+\frac{1}{4}T+\frac{1}{16}T+\frac{1}{64}T+\cdots \\ & =(1+\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\cdots )T\end{array}$$

Now Archimedes only has to sum this series. For us moderns this is no trouble: we recognize this immediately as a geometric series

But why is it called geometric? Well (this is not the only reason, but…) Archimedes was the first human to sum such a series, and he did so completely geometrically. Ignoring the leading $1$, we can interpret all the fractions as proportions of the area of a square. The first term $1/4$ tells us to take a quarter of the square, the next term says to take a quarter of a quarter more, and so on. Repeating this process infinitely, Archimedes ends up with the following figure, where the highlighted squares on the diagonal represent the completed infinite sum.

The infinite process: $1/4+1/16+1/64+\cdots$

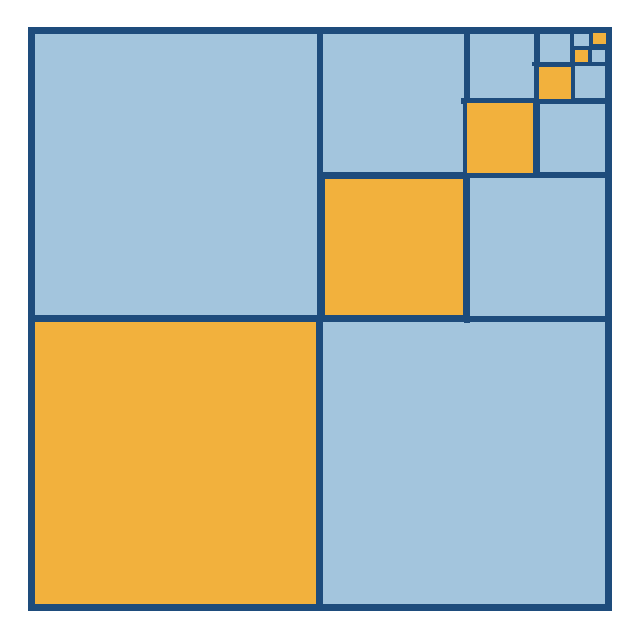
He then notes that this is precisely one third the area of the bounding square, as two more identical copies of this sequence of squares fill it entirely (just slide our squares to the left, or down). Thus, this infinite sum is precisely $1/3$, and so the total area is $1$ plus this, or $4/3$.

This tells us an important fact, beyond just the area of the parabola we sought! We were looking to compute the area of a curved shape, and the procedure we found could never give us the answer exactly, but only an infinite sequence of better approximations. Being acquainted with the work of Pythagoras and the Babylonians, this might have well led us to conjecture that the area of the parabola must be irrationally related to the area of the triangle. But Archimedes showed this is not the case; our infinite sum here evaluates to a rational number, $4/3$!

Infinite sequences of rational numbers can sometimes produce a wholly new number, and sometimes just converge to another rational.*

How can we tell? This is one motivating reason to develop a rigorous study of such objects. But it gets even more important, if we try to generalize Archimedes’ argument.

Troubles with Geometric Series

Archimedes’ quadrature of the parabola represents a monumental leap forward in human history. This is the first time in the mathematical literature where infinity is not treated as some distant ideal, but rather a real place that can be reached. And the argument itself is an absolute classic - involving the first occurrence of an infinite series in mathematics, and a wonderfully geometric summation method (hence the name geometric series, which survives until today). The elegance of Archimedes’ calculation is almost dangerous - its easy to be blinded by its apparent simplicity, and – like Icarus – fly too close to the sun, falling from these heights of logic directly into contradiction.

Archimedes visualized his argument for the sum $\sum \frac{1}{4^n}$ as though it was occurring inside of a larger square, but there’s another perspective we could take. Call the total sum $S$, $$S=1+\frac{1}{4}+\frac{1}{4^2}+\frac{1}{4^3}+\cdots$$

and note that multiplying $S$ by $1/4$ is the same as removing the first term, as it shifts all the terms down by one space:

$$\frac{1}{4}S=\frac{1}{4}+\frac{1}{4^2}+\frac{1}{4^3}+\frac{1}{4^4}+\cdots =S-1$$

Thus, $\frac{1}{4}S=S-1$, and we can solve this algebraic equation directly to find $S=4/3$. The beauty of this argument is that unlike Archimedes’ original, its not tied to the number $1/4$ at all! Imagine we took some number $r$, and we wanted to add up the infinite sum $$1+r+r^2+r^3+r^4+r^5+r^6+r^7+\cdots +r^n+\cdots$$

Call that sum $S$, and notice that we have the same property, multiplying the sum by $r$ shifts every term down by one, so we get the same result as if we just removed the first term:

$$rS=S-1$$

We can then solve this for $S$ and get

$$S=\frac{1}{1-r}$$

This gives us what we expect when $r=1/4$, and trying it for other fractions, like $r=1/5$ or $r=23/879$, we can confirm (with the help of a computer) that the infinite sum really does approach the value this formula gives!

Amazingly, it even works for negative numbers, after we think about what this means. If $r=\frac{-1}{2}$ then

$$1+r+r^2+r^3+r^4+r^5+\cdots =1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\frac{1}{16}-\cdots$$

Using our formula above we see that this is supposed to converge to $$S=\frac{1}{1-\left(\frac{-1}{2}\right)}=\frac{1}{1+\frac{1}{2}}=\frac{1}{\frac{3}{2}}=\frac{2}{3}$$

And, using a computer to add up the first 100 terms we see

$$S\approx 0.66666666666666666666666666666692962030174033726847057618$$

This is pretty incredible, as our original geometric reasoning doesn’t make sense for $r=-1/2$, but the algebra works just fine! We may also wish to investigate what happens when $r=1$, which would give $$S=1+1+1+1+1+1+\cdots$$

This is going off to infinity, and our formula gives $S=1/(1-1)=1/0$, which could make sense: we could even take this as an indication that we should define $1/0=\mathrm{\infty }$. But things get more interesting with $r=-1$. Here the sum is

$$S=1-1+1-1+1-1+1-1+1-1+1-\cdots$$

As we add this up term by term, we first have 1, then 0, then 1 then 0, over and over agan as we repeatedly add a 1, and then immediately cancel it out. This isn’t getting close to any number at all! But our formula gives

$$S=\frac{1}{1-(-1)}=\frac{1}{2}$$

Now we have a real question - did we just discover a new, deep fact of mathematics - that we can sensibly assign values to series like this, that we weren’t originally concerned with, or did we discover a limitation of our theorem? This is an interesting, and important question to come out of our playing around!

Thus far, we haven’t seen any cases where our theorem has output any ‘obviously’ wrong answers, so we may be inclined to trust it. But this does not hold up to further scrutiny: what about when $r=2$? Here the sum is

$$1+2+4+8+16+32+\cdots$$

which is clearly going to infinity. But our formula disagrees, as it would have you belive the sum is $S=1/(1-2)=-1$. This raises the more general problem: when working with infinity, sometimes a formula you derive works, and sometimes it doesn’t. How can you tell when to trust it?

Exercise 6 Explain what goes wrong with the argument when $r=2$…

The Circle Constant

The curved shape that everyone was really interested in was not the parabola, but the circle. Archimedes tackles this in his paper The Measurement of the Circle, where he again constructs a finite sequence of approximations built from triangles, and then reasons about the circle out at infinity. First, we need a definition:

Definition 3 ($\pi$ and $\tau$) The area of the unit circle is denoted by the constant $\pi$. The circumference of the unit circle is denoted by the constant $\tau$.

Archimedes came up with a sequence of overestimates, and underestimates for $\pi$ by inscribing and circumscribing regular polygons.

Circumscribed polygons provide an overestimate of the area of the circle.

Inscribed polygons provide an underestimate of the area of the circle.

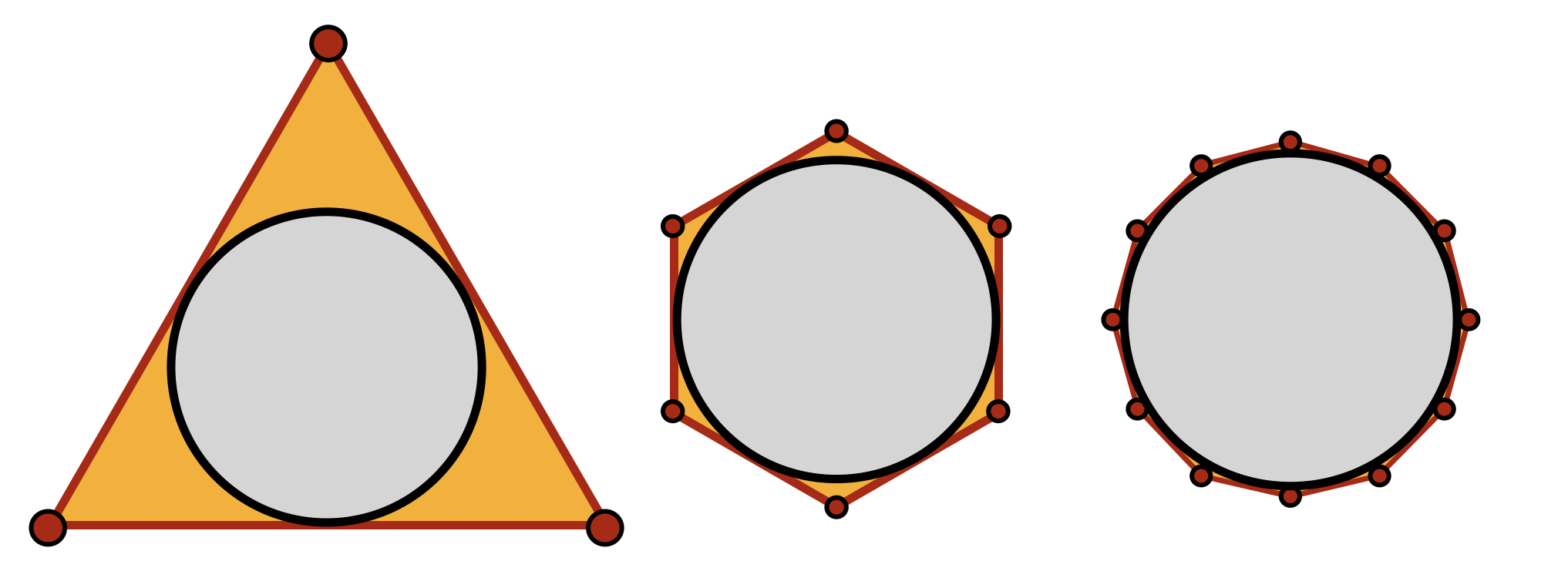
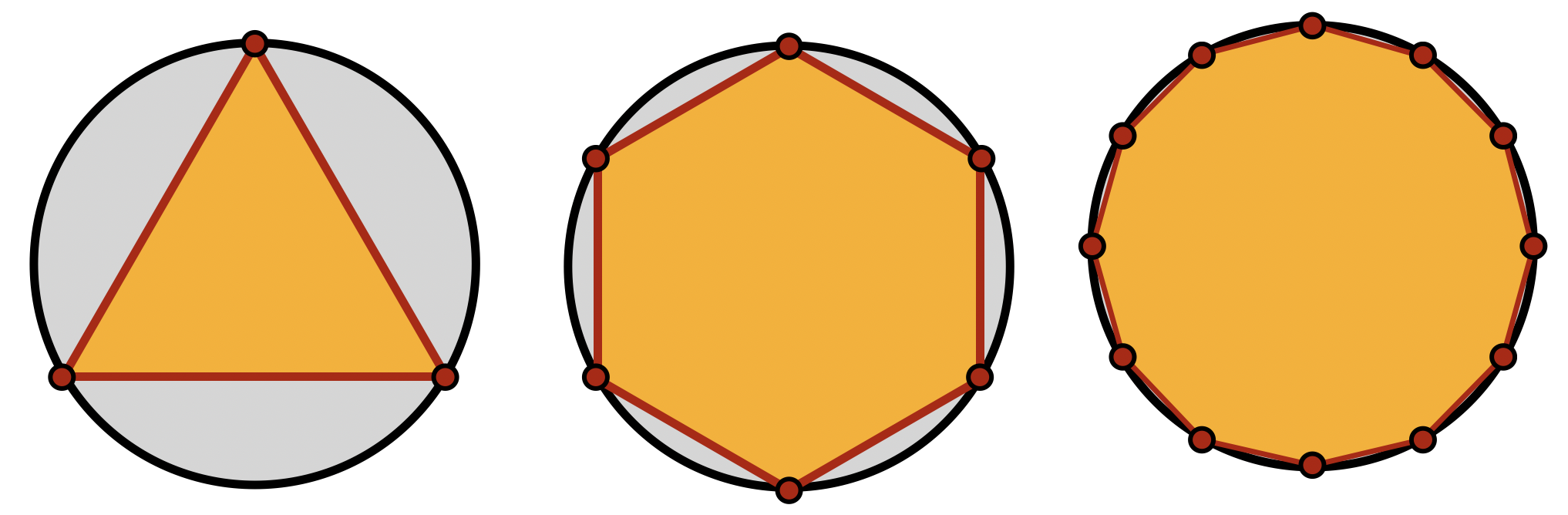
Any polygon inside the unit circle gave an underestimate, and any polygon outside gave an overestimate. The more sides the polygon had, the better the approximations would be.

Calculating the area and perimeter of regular $n$-gons is (theoretically) straightforward, as they can be decomposed into $2n$ right triangles. Drawing a diagram, we find the relations below;

Decomposing a circumscribed polygon into right triangles.

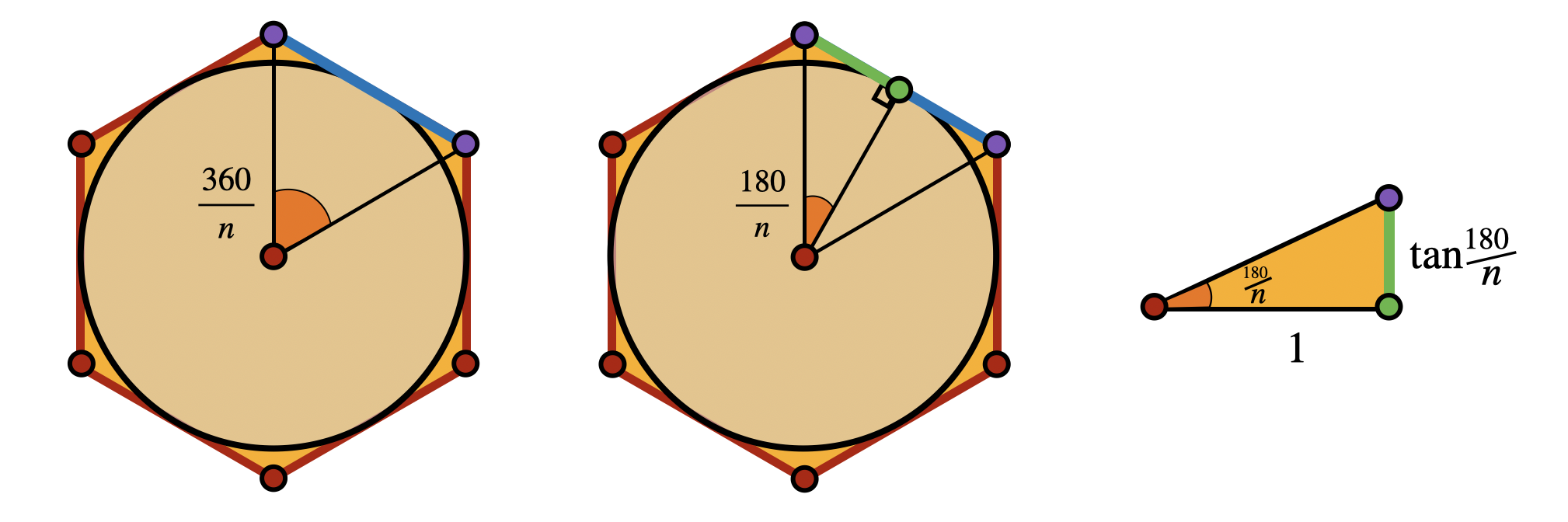
Proposition 2 (Area of a Circumscribed Polygon) The area of a regular $n$-gon circumscribing the unit circle is given by $$\begin{array}{rl}{C}_n& =2n\cdot (\frac{1}{2}\cdot 1\cdot \tan \frac{180}{n})\\ & =n\tan \frac{180}{n}\end{array}$$

Proposition 3 (Perimeter of a Circumscribed Polygon) The perimeter of a regular $n$-gon circumscribing the unit circle is given by $$P_n=2n\cdot \tan \frac{180}{n}$$

Decomposing an inscribed polygon into right triangles.

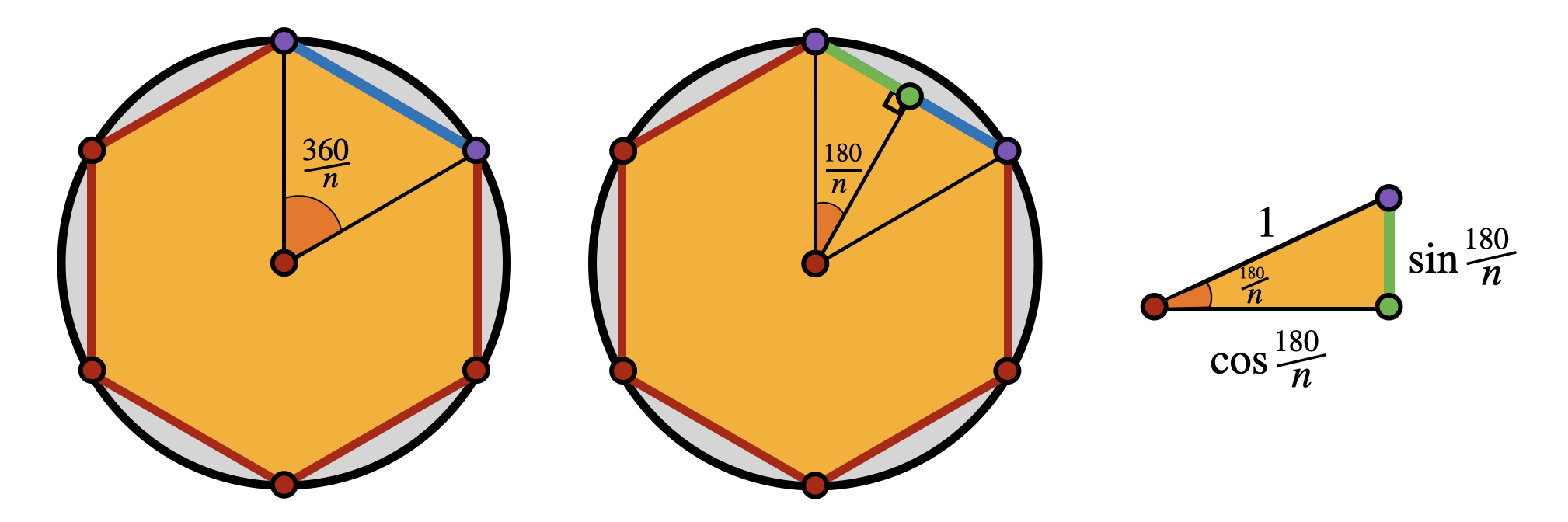
Proposition 4 (Area of a Inscribed Polygon) The area of a regular $n$-gon inscribed in the unit circle is given by $$\begin{array}{rl}{a}_n& =2n\cdot (\frac{1}{2}\cdot \cos \frac{180}{n}\cdot \sin \frac{180}{n})\\ & =\frac{n}{2}\sin \frac{360}{n}\end{array}$$

Where we used the trigonometric identity $\sin (2x)=2\sin x\cos x$ to simplify $a_n$ above.

Proposition 5 (Perimeter of a Inscribed Polygon) The perimeter of a regular $n$-gon inscribed in the unit circle is given by $$p_n=2n\cdot \sin \frac{180}{n}$$

Using these, Archimedes calculated away all the way to the 96-gon, which provided him with the estimates

$$\frac{223}{71}<\pi <\frac{22}{7}$$

This was the best estimate of $\pi$ calculated during the classical period of the Greeks, but the same method was applied by Chinese mathematician Zu Chongzi in the 400s CE to much much larger polygons.
Working with the $24,576$-gon, he found

$$\frac{355}{113}<\pi <\frac{22}{7}$$

The lower bound here, $355/113$ is the best possible rational approximation of $\pi$ with denominator less than four digits, and equals $3.14159292\cdots$, whereas $\pi =3.14159265\cdots$. This was the most accurate approximate to $\pi$ calculated anywhere in the world for over 800 years, and was only surpassed in the late 1300s by Indian mathematician Madhava, about whom we’ll learn more soon.

Remark 1. The next best rational approximation is $\frac{52163}{16604}$, which is a significantly more complicated looking fraction!

Proving $\tau =2\pi$

While impressive, Archimedes’ main goal was not the approximate calculation above, but rather an exact theorem. He wanted to understand the true relationship between the area and perimeter of the circle, and wished to use these approximations as a guide to what is happening with the real circle, “out at infinity”.

To understand this case, Archimedes argues that as $n$ goes to infinity, the sequences of inscribed and circumscribed polygons approach the circle, and so in the limit, the sequences of areas must tend to the area of the circle ($\pi$) and the sequences of perimeters must tend to the perimeter of the circle ($\tau$).

$$A_n\to \pi P_n\to \tau$$

But, now look carefully at the form of the expressions we derived for the circumscribing polygons in Proposition 2 and Proposition 3: $$A_n=n\cdot \tan \frac{180}{n}{P}_n=2n\cdot \tan \frac{180}{n}$$

Here, we do not need to worry about explicitly calculating $A_n$ or $P_n$; all we need to notice is that the perimeter is exactly twice the area, $P_n=2A_n$! This makes sense:

• Each polygon is built out of $n$ triangles.
• The area of a triangle is half its base times its height
• The height of each triangle is 1 (the radius of the circle)
• Thus, the area the sum of half all the bases, or half the perimeter!

But since this exact relationship holds for every single value of $n$, Archimedes argued it must also be true in the limit, so the perimeter is twice the area:

Theorem 3 (Archimedes) $$\tau =2\pi$$

Troubles With Limits

Archimedes again leaves us with an argument so elegant and deceptively simple that its easy to under-appreciate its subtlety and immediately fall prey to contradiction. What if we attempt to repeat Archimedes argument, but with a different sequence of polygons approaching the circle?

Remark 2. To be fair to the master, Archimedes is much, much more careful in his paper than I was above, so part of the apparent simplicity is a consequence of my omission.

For example, what if we start with a square circumscribing the circle, and then at each stage produce a new polygon with the following rule:

• At each corner of the polygon, find the largest square that fits within the polygon, and remains outside the circle. Then remove this square.

Iteratively removing the largest square outside the circle at each vertex produces a sequence of right angled polygons which converges to the circle.

Exactly like in Archimedes’ example this sequence of polygons approaches the circle as we repeat over and over. In fact, in the limit - this sequence literally becomes the circle (meaning that after infinitely many steps, there are no points of the resulting shape remaining outside the circle at all). Thus, just as for our original sequence of polygons, we expect that the areas and perimeters of these shapes approach the areas and perimeters of the circle itself. That is,

$$A_n\to \pi ,P_n\to \tau$$

While the behavior of $A_n$ takes a bit of work to understand, this sequence of polygons is constructed to make analyzing the perimeters particularly nice. Look what happens at each stage near a dent: two edges are turned inward to the circle, but do not change in length.

Removing a square at a vertex does not change the perimeter of the polygon, as it replaces two segments with two other segments of the same length.

Since adding a dent does not change the length of the perimeter, each polygon in our sequence has exactly the same perimeter as the original! The original perimeter is easy to calculate, each side of the square is a diameter of the unit circle, so its total perimeter is 8. But since this both does not change and converges in the limit to the circles circumference, we have just derived the amazing fact that

$$\tau =8$$

This is inconsistent with what we learn from Archimedes’ argument which shows that $\pi <22/7$ and $\tau =2\pi$, so $\tau <44/7=6.2857\dots$. It appears that we have applied the same argument twice, and found a contradiction in comparing the results!

Exercise 7 (Convergence to the Diagonal) We can run an argument analogous to the above which proves that $\sqrt{2}=2$, by looking at a sequence of polygons that converge to a right triangle with legs of length $1$. Let $T_0$ denote the unit square, and $T_n$

Prove that as $n$ goes to infinity the area of the polygons $T_n$ do converge to the area of the triangle (Hint: can you write down a formula for the total error between $T_n$ and the triangle?) Also, prove that the length of the zig-zag diagonal side of the $T_n$ has length $2$ always, independent of $n$. Thus, the limit of the zigzag, which becomes the hypotenuse of the triangle, has length 2!

But the pythagorean theorem tells us that its length must be $\sqrt{1^2+1^2}=\sqrt{2}$, so in fact we have proven $\sqrt{2}=2$, or $2=4$, a contradiction in mathematics.

Its quite difficult to pinpoint exactly what goes wrong here, and thus this presents a particularly strong argument for why we need analysis: without a rigorous understanding of infinite processes and limits, we can never be sure if our seemingly reasonable calculations give the right answers, or lies!

Estimating $\pi$

With our modern access to calculator technology, the trigonometric formulas above essentially solves the problem: for example, plug in $n=96$ to a calculator (set to degrees!) to replicate the work of Archimedes in one click.

But this poses a historical problem: of course the ancients did not have a calculator, so how did they compute such accurate approximations millennia ago? And there’s also a potential logical problem lurking in the background: inside our calculator there is some algorithm computing the trigonometric functions, and perhaps that algorithm depends on already knowing something about the value of $\pi$. If so, using this calculator to give a from-first-principles estimate of $\pi$ would be circular!

To compute their estimates, both Archimedes and Zu Chongzi landed on an idea similar to the Babylonians and their computation of $\sqrt{2}$: they found an iterative procedure that starts with one polygon, and doubles its number of sides. With such a procedure in hand, they could start with any polygon and rapidly scale it up to better and better estimates. Beginning with an hexagon, Archimedes only needed to double four times:

$$6\to 12\to 24\to 48\to 96$$

Exercise 8 (The Doublings of Zu Chongzi) How many times did Zu Chongzi double the sides of a hexagon to reach the 24,576 gon?

Following Archimedes, we’ll look at the doubling procedure for the perimeter of inscribed polygons: given $p_n$ we seek a method to compute $p_{2n}$. By the formula in Proposition 4, it is enough to be able to compute $\sin (360/(2n))$ in terms of $\sin (360/n)$, that is, we need to be able to compute the sine of half the angle. The half-angle identities from trigonometry prove helpful here:

Definition 4 (Half Angle Identities) $$\cos \left(\frac{\theta }{2}\right)=\sqrt{\frac{1+\cos \theta }{2}}\sin \left(\frac{\theta }{2}\right)=\sqrt{\frac{1-\cos \theta }{2}}$$ $$\tan \left(\frac{\theta }{2}\right)=\sqrt{\frac{1-\cos \theta }{1+\cos \theta }}=\frac{\sin \theta }{1-\cos \theta }=\frac{1-\cos \theta }{\sin \theta }$$

Also making use of the pythagorean identity ${\sin }^2\theta +{\cos }^2\theta =1$, we can compute as follows:

$$\begin{array}{rl}\sin \frac{\theta }{2}& =\sqrt{\frac{1-\cos \theta }{2}}\\ & =\sqrt{\frac{1-\sqrt{{\cos }^2\theta }}{2}}\\ & =\sqrt{\frac{1-\sqrt{1-{\sin }^2\theta }}{2}}\end{array}$$

Lets write $s_n=\sin (180/n)$ for brevity. Then, the above formula tells us how to compute $s_{2n}$ if we know $s_n$:

$$s_{2n}=\sqrt{\frac{1-\sqrt{1-s_n^2}}{2}}$$

This sort of relationship is called a recurrence relation, or a recursively defined sequence as it tells us how to compute the next term in the sequence if we have the previous one. Notice there are no more trigonometric formulas in the recurrence - so if we can find the value $s_n$ for any polygon, we can start with that, and iteratively double.

Example 2 (A Recurrence for $p_n$) By Proposition 5, we see that $p_n=2n{s}_n$. Thus $p_{2n}=2(2n)s_{2n}=4s_{2n}$, and using the recurrence for $s_{2n}$ we see $$\begin{array}{rl}{p}_{2n}& =4n{s}_{2n}\\ & =4n\sqrt{\frac{1-\sqrt{1-s_n^2}}{2}}\\ & =2n\sqrt{2-2\sqrt{1-s_n^2}}\\ & =2n\sqrt{2-\sqrt{4-4s_n^2}}\end{array}$$

But, since $s_n=p_n/(2n)$, substituting this in gives a relation between $p_{2n}$ and $p_n$ directly:

$$\begin{array}{rl}{p}_{2n}& =2n\sqrt{2-\sqrt{4-4s_n^2}}\\ & =2n\sqrt{2-\sqrt{4-{\left(\frac{p_n}{n}\right)}^2}}\end{array}$$

The incredible fact: even though we used trigonometry to derive this recurrence, we do not need to know how to evaluate any trigonometric functions to actually use it! All we need to be able to do is find the perimeter of some inscribed $n$-gon, and then we can repeatedly double over and over!

But how can we get started? A beautiful observation of Archimedes was that a regular hexagon inscribed in the circle has perimeter exactly equal to 6, as it can be decomposed into six equilateral triangles, whose side length is the circle’s radius. And with that, we are off!

Example 3 (The Perimeter of an Inscribed 96-gon) Since $p_6=6$, we begin with a doubling to find $p_{12}:$ $$\begin{array}{rl}{p}_{12}& =12\sqrt{2-\sqrt{4-{\left(\frac{6}{6}\right)}^2}}\\ & =12\sqrt{2-\sqrt{3}}\end{array}$$

Using this, we know $\frac{p_{12}}{12}=\sqrt{2-\sqrt{3}}$, and we can double again:

$$\begin{array}{rl}{p}_{24}& =24\sqrt{2-\sqrt{4-(2-\sqrt{3})}}\\ & =24\sqrt{2-\sqrt{2+\sqrt{3}}}\end{array}$$

Now doubling to the 48 gon,

$$\begin{array}{rl}{p}_{48}& =48\sqrt{2-\sqrt{4-(2-\sqrt{2+\sqrt{3}})}}\\ & =48\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\end{array}$$

One more doubling brings us to the 96-gon, $$p_{96}=96\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}}$$

Numerically approximating this gives 6.282063901781019276222, which is more recognizable to us if we compute the half perimeter:

$$\frac{p_{96}}{2}\approx 3.141031950890\dots$$

Exercise 9 Find a recurrence relation for the area $a_{2n}$ of the inscribed polygon, in terms of the area $a_n$ of a polygon with half as many sides.

Exercise 10 Let $t_n=\tan (180/n)$. Show that $t_n$ satisfies the recurrence relation $$t_{2n}=\sqrt{1+\frac{1}{t_n^2}}-\frac{1}{t_n}$$

Hint: you’ll need some trig identities to write everything in terms of tangent! Use this to find a recurrence relation for $P_n$. Can you use this to find the circumference of an octagon circumscribing the unit circle?

After all of this are still left with a fundamental question: what sort of number is $\pi$? Archimedes’ calculation out at infinity showed the area and circumference of a circle were related, but did not give us an exact value for either. These approximate calculations lead to some pretty scary looking numbers, but we know better than to trust that: we’ve already seen an infinite series of archimedes that summed to a nice rational number, and soon we will meet a nested sequence of square roots that collapses to a single root at infinity:

$$\sqrt{1+\sqrt{1+\sqrt{1+\cdots }}}=\frac{1+\sqrt{5}}{2}$$

Convergence, Concern and Contradiction

Madhava, Leibniz & $\pi /4$

Madhava was a Indian mathematician who discovered many infinite expressions for trigonometric functions in the 1300’s, results which today are known as Taylor Series after Brook Taylor, who worked with them in 1715. In a particularly important example, Madhava found a formula to calculate the arc length along a circle, in terms of the tangent: or phrased more geometrically, the arc of a circle contained in a triangle with base of length $1$.

The first term is the product of the given sine and radius of the desired arc divided by the cosine of the arc. The succeeding terms are obtained by a process of iteration when the first term is repeatedly multiplied by the square of the sine and divided by the square of the cosine. All the terms are then divided by the odd numbers 1, 3, 5, …. The arc is obtained by adding and subtracting respectively the terms of odd rank and those of even rank.

As an equation, this gives

$$\theta =\frac{\sin \theta }{\cos \theta }-\frac{1}{3}\frac{{\sin }^2\theta }{{\cos }^2\theta }\left(\frac{\sin \theta }{\cos \theta }\right)+\frac{1}{5}\frac{{\sin }^2\theta }{{\cos }^2\theta }\left(\frac{{\sin }^2\theta }{{\cos }^2\theta }\frac{\sin \theta }{\cos \theta }\right)+\cdots$$

$$=\tan \theta -\frac{{\tan }^3\theta }{3}+\frac{{\tan }^5\theta }{5}-\frac{{\tan }^7\theta }{7}+\frac{{\tan }^9\theta }{9}-\cdots$$

If we take the arclength $\pi /4$ (the diagonal of a square), then both the base and height of our triangle are equal to $1$, and this series becomes

$$\frac{\pi }{4}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$

This result was also derived by Leibniz (one of the founders of modern calcuous), using a method close to something you might see in Calculus II these days. It goes as follows: we know (say from the last chapter) the sum of the geometric series

$$\sum _{n\ge 0}{r}^n=\frac{1}{1-r}$$

Thus, substituting in $r=-x^2$ gives

$$\sum _{n\ge 0}(-1{)}^n{x}^{2n}=\frac{1}{1+x^2}$$

and the right hand side of this is the derivative of arctangent! So, anti-differentiating both sides of the equation yields

$$\begin{array}{rl}\arctan x& =\int \sum _{n\ge 0}(-1{)}^n{x}^{2n}dx\\ & =\sum _{n\ge 0}\int (-1{)}^n{x}^{2n}dx\\ & =\sum _{n\ge 0}(-1{)}^n\frac{x^{2n+1}}{2n+1}\end{array}$$

Finaly, we take this result and plug in $x=1$: since $\arctan (1)=\pi /4$ this gives what we wanted:

$$\frac{\pi }{4}=\sum _{n\ge 0}(-1{)}^n\frac{1}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots$$

This argument is completely full of steps that should make us worried:

• Why can we substitute a variable into an infinite expression and ensure it remains valid?
• Why is the derivative of arctan a rational function?
• Why can we integrate an infinite expression?
• Why can we switch the order of taking an infinte sum, and integration?
• How do we know which values of $x$ the resulting equation is valid for?

But beyond all of this, we should be even more worried if we try to plot the graphs of the partial sums of this supposed formula for the arctangent.

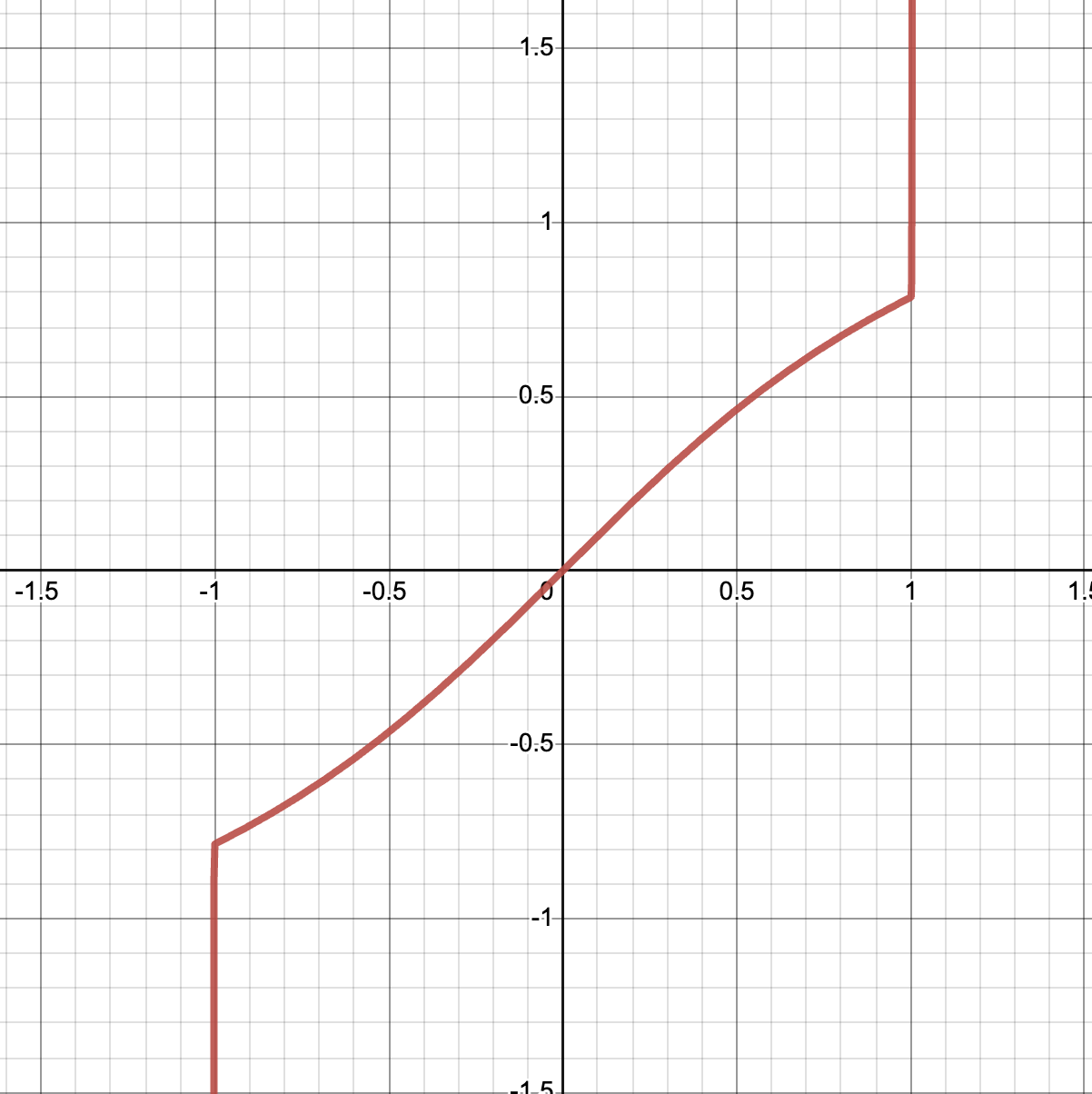
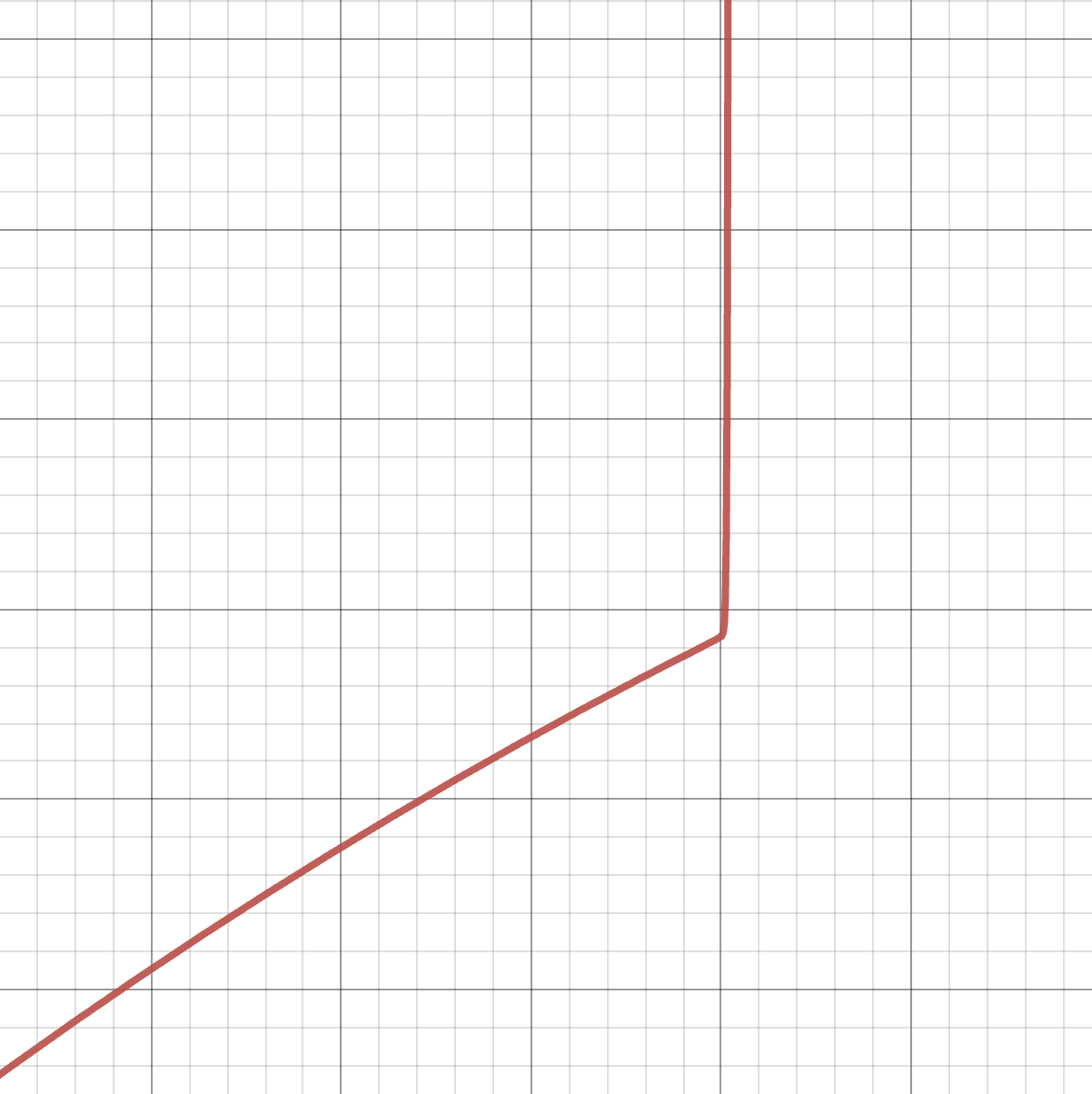
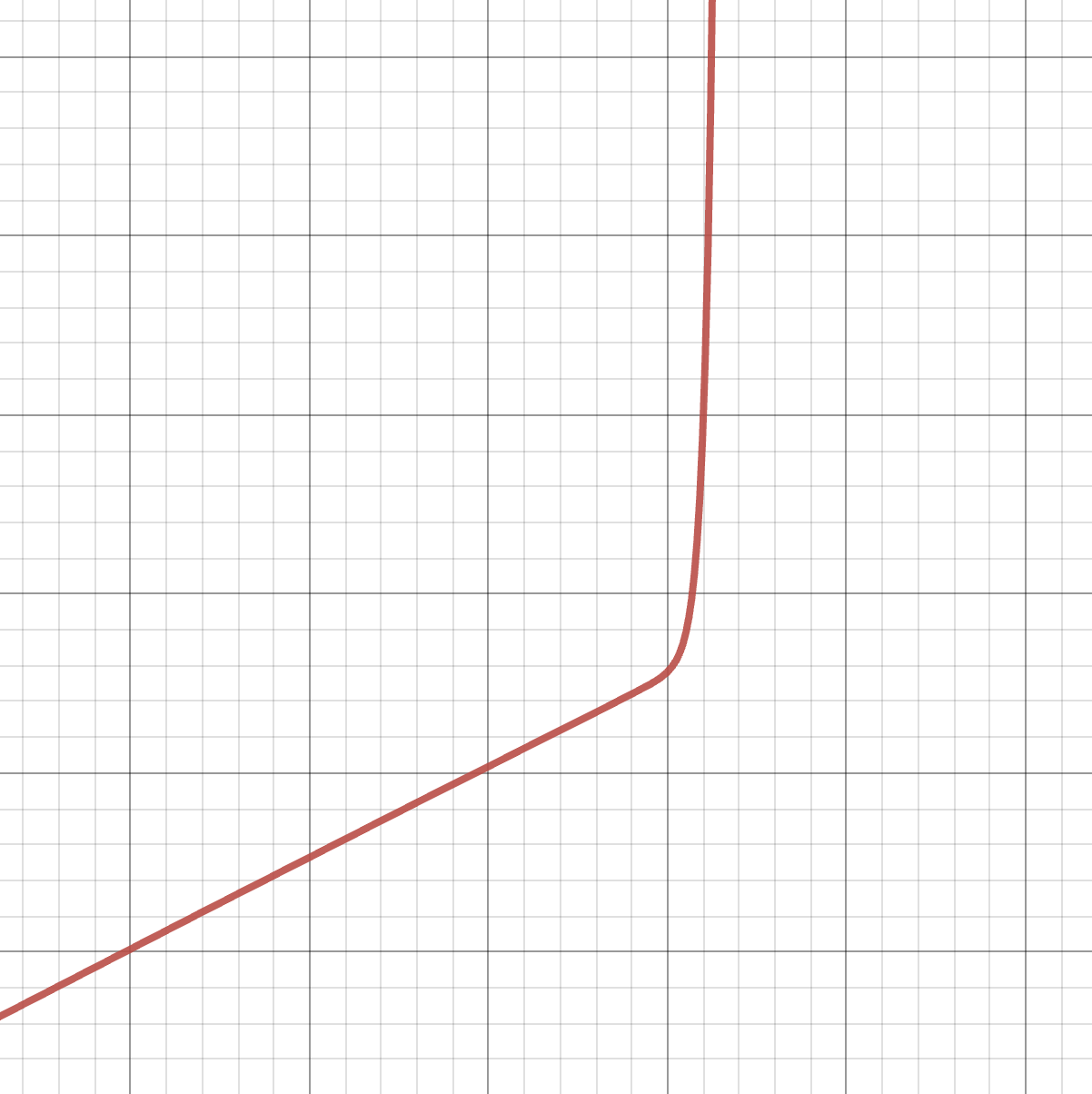
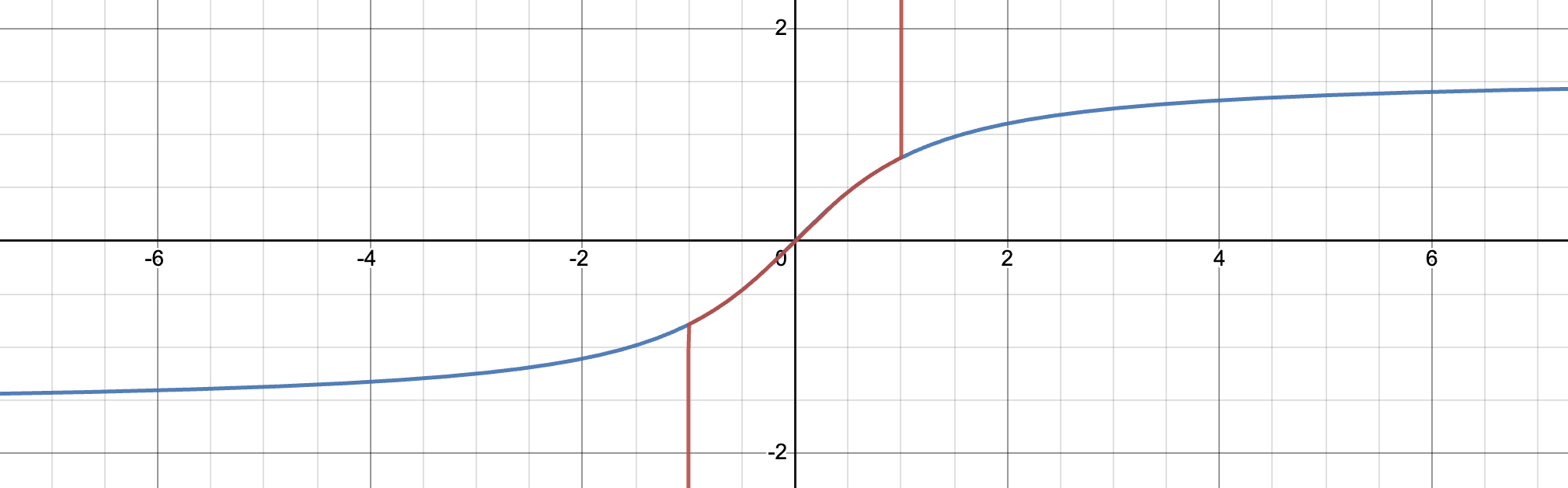
The infinite series we derived seems to match the arctangent exactly for a while, and then abruptly stop, and shoot off to infinity. Where does it stop? *Right at the point we are interested in, $\theta =\pi /4$, so $\tan (\theta )=1$. So, even a study of which intervals a series converges in will not be enough here, we need a theory that is so precise, it can even tell us exactly what happens at the single point forming the boundary between order and chaos.

And perhaps, before thinking the eventual answer might simply say the series always converges at the endpoints, it turns out at the other endpoint $x=-1$, this series itself diverges! So whatever theory we build will have to account for such messy cases.

Dirichlet & $\log 2$

In 1827, Dirichlet was studying the sums of infinitely many terms, thinking about the alternating harmonic series $$\sum _{n\ge 1}\frac{(-1{)}^n}{n+1}$$

Like the previous example, this series naturally emerges from manipulations in calculus: beginning once more with the geometric series $\sum _{n\ge 0}{r}^n=\frac{1}{1-r}$. We substitute $r=-x$ to get a series for $1/(1+x)$ and then integrate term by term to produce a series for the logarithm:

$$\log (1+x)=\int \frac{1}{1+x}dx=\int \sum _{n\ge 0}(-1{)}^n{x}^n$$

$$=\sum _{n\ge 0}(-1{)}^n\frac{x^{n+1}}{n+1}=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots$$

Finally, plugging in $x=1$ yields the sum of interest. It turns out not to be difficult to prove that this series does indeed approach a finite value after the addition of infinitely many terms, and a quick check adding up the first thousand terms gives an approximate value of $0.6926474305598$, which is very close to $\log (2)$ as expected..

$$\log (2)=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\frac{1}{7}-\frac{1}{8}+\frac{1}{9}-\frac{1}{10}\cdots$$

What happens if we multiply both sides of this equation by $2$?

$$2\log (2)=2-1+\frac{2}{3}-\frac{1}{2}+\frac{2}{5}-\frac{1}{3}+\frac{2}{7}-\frac{1}{4}+\frac{2}{9}-\frac{1}{5}\cdots$$

We can simplify this expression a bit, by re-ordering the terms to combine similar ones:

$$\begin{array}{rl}2\log (2)& =(2-1)-\frac{1}{2}+(\frac{2}{3}-\frac{1}{3})-\frac{1}{4}+(\frac{2}{5}-\frac{1}{5})-\cdots \\ & =1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots \end{array}$$

After simplifying, we’ve returned to exactly the same series we started with! That is, we’ve shown $2\log (2)=\log (2)$, and dividing by $\log (2)$ (which is nonzero!) we see that $2=1$, a contradiction!

What does this tell us? Well, the only difference between the two equations is the order in which we add the terms. And, we get different results! This reveals perhaps the most shocking discovery of all, in our time spent doing dubious computations: infinite addition is not always commutative, even though finite addition always is.

Here’s an even more dubious-looking example where we can prove that $0=\log 2$. First, consider the infinite sum of zeroes:

$$0=0+0+0+0+0+\cdots$$

Now, rewrite each of the zeroes as $x-x$ for some specially chosen $x$s:

$$0=(1-1)+(\frac{1}{2}-\frac{1}{2})+(\frac{1}{3}-\frac{1}{3})+(\frac{1}{}-\frac{1}{4})+\cdots$$

Now, do some re-arranging to this:

$$(1+\frac{1}{2}-1)+(\frac{1}{3}+\frac{1}{4}-\frac{1}{2})+(\frac{1}{5}+\frac{1}{6}-\frac{1}{3})+\cdots$$

Make sure to convince yourselves that all the same terms appear here after the rearrangement!

Simplifying this a bit shows a pattern:

$$(1-\frac{1}{2})+(\frac{1}{3}-\frac{1}{4})+(\frac{1}{5}-\frac{1}{6})+\cdots$$

Which, after removing the parentheses, is the familiar series $\sum \frac{(-1{)}^n}{n}$. But this series equals $\log (2)$ (or, was it $2\log 2$?) So, if we are to believe that arithmetic with infinite sums is valid, we reach the contradiction

$$0=\log 2$$

Infinite Expressions in Trigonometry

The sine function (along with the other trigonometric, exponential, and logarithmic functions) differs from the common functions of early mathematics (polynomials, rational functions and roots) in that it is defined not by a formula but geometrically.

Such a definition is difficult to work with if one actually wishes to compute: for example, Archimedes after much trouble managed to calculate the exact value of $\sin (\pi /96)$ using a recursive doubling procedure, but he would have failed to calculate $\sin (\pi /97)$ - 97 is not a multiple of a power of 2, so his procedure wouldn’t apply! The search for a general formula that you could plug numbers into and compute their sine, was foundational to the arithmetization of geometry.

One big question about this procedure is why in the world should this work? We found a function that $\sin (x)$ satisfies, and then we plugged something else into that function and started iterating: what justification do we have that this should start to approach the sine? We can check after the fact that it (seems to have) worked, but this leaves us far from any understanding of what is actually going on. –>

Infinite Product of Euler

One famous infinite expression for the sine function arose from thinking about the behavior of polynomials, and the relation of their formulas to their roots. As an example consider a quartic polynomial $p(x)$ with roots at $x=a,b,c,d$. Then we can recover $p$ up to a constant multiple as a product of linear factors with roots at $a,b,c,d$. If the $y-$intercept is $p(0)=k$, we can give a fully explicit description

$$p(x)=k(1-\frac{x}{a})(1-\frac{x}{b})(1-\frac{x}{c})(1-\frac{x}{d})$$

In 17334, Euler attempted to apply this same reasoning in the infinite case to the trigonometric function $\sin (x)$. This has roots at every integer multiple of $\pi$, and so following the finite logic, should factor as a product of linear factors, one for each root. There’s a slight technical problem in directly applying the above argument, namely that $\sin (x)$ has a root at $x=0$, so $k=0$. One work-around is to consider the function $\frac{\sin x}{x}$. This is not actually defined at $x=0$, but one can prove $\underset{x\to 0}{lim}\frac{\sin x}{x}=1$, and attempt to use $k=1$

GRAPH

Its roots agree with that of $\sin (x)$ except there is no longer one at $x=0$. That is, the roots are $\dots ,-3\pi ,-2\pi ,-\pi ,\pi ,2\pi ,3\pi ,\dots$, and the resulting factorization is

$$\frac{\sin x}{x}=\cdots (1+\frac{x}{3\pi })(1+\frac{x}{2\pi })(1+\frac{x}{\pi })(1-\frac{x}{\pi })(1-\frac{x}{2\pi })(1-\frac{x}{3\pi })\cdots$$

Euler noticed all the factors come in pairs, each of which represented a difference of squares.

$$(1-\frac{x}{n\pi })(1+\frac{x}{2n\pi })=(1-\frac{x^2}{n^2{\pi }^2})$$

Not worrying about the fact that infinite multiplication may not be commutative (a worry we came to appreciate with Dirichlet, but this was after Euler’s time!), we may re-group this product pairing off terms like this, to yield

$$\frac{\sin x}{x}=(1-\frac{x^2}{{\pi }^2})(1-\frac{x^2}{2^2{\pi }^2})(1-\frac{x^2}{3^2{\pi }^2})\cdots$$

Finally, we may multiply back through by $x$ and get an infinite product expression for the sine function:

Proposition 6 (Euler) $$\sin x=x(1-\frac{x^2}{{\pi }^2})(1-\frac{x^2}{4{\pi }^2})(1-\frac{x^2}{9{\pi }^2})\cdots$$

This incredible identity is actually correct: there’s only one problem - the argument itself is wrong!

Exercise 11 In his argument, Euler crucially uses that if we know

• all the zeroes of a function
• the value of that function is 1 at $x=0$

then we can factor the function as an infinite polynomial in terms of its zeroes. This implies that a function is completely determined by its value at $x=0$ and its zeroes (because after all, once you know that information you can just write down a formula like Euler did!) This is absolutely true for all finite polynomials, but it fails spectacularly in general.

Show that this is a serious flaw in Euler’s reasoning by finding a different function that has all the same zeroes as $\sin (x)/x$ and is equal to $1$ at zero (in the limit)!

Exercise 12 (The Wallis Product for $\pi$) In 1656 John Wallis derived a remarkably beautiful formula for $\pi$ (though his argumnet was not very rigorous).

$$\frac{\pi }{2}=\frac{2}{1}\frac{2}{3}\frac{4}{3}\frac{4}{5}\frac{6}{5}\frac{6}{7}\frac{8}{7}\frac{8}{9}\frac{10}{9}\frac{10}{11}\frac{12}{11}\frac{12}{13}\cdots$$

Using Euler’s infinite product for $\sin (x)$ evaluated at $x=\pi /2$, give a derivation of Wallis’ formula.

The Basel Problem

The Italian mathematician Pietro Mengoli proposed the following problem in 1650:

Definition 5 (The Basel Problem) Find the exact value of the infinite sum $$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\cdots$$

By directly computing the first several terms of this sum one can get an estimate of the value, for instance adding up the first 1,000 terms we find $1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots \frac{1}{1,{000}^2}=1.6439345\dots$, and ading the first million terms gives

$$1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{1,{000}^2}+\cdots +\frac{1}{1,000,{000}^2}=1.64492406\dots$$

so we might feel rather confident that the final answer is somewhat close to 1.64. But the interesting math problem isn’t to approximate the answer, but rather to figure out something exact, and knowing the first few decimals here isn’t of much help.

This problem was attempted by famous mathematicians across Europe over the next 80 years, but all failed. All until a relatively unknown 28 year old Swiss mathematician named Leonhard Euler published a solution in 1734, and immediately shot to fame. (In fact, this problem is named the Basel problem after Euler’s hometown.)

Proposition 7 (Euler) $$\sum _{n\ge 1}\frac{1}{n^2}=\frac{{\pi }^2}{6}$$

Euler’s solution begins with two different expressions for the function $\sin (x)/x$, which he gets from the sine’s series expansion, and his own work on the infinite product:

$$\begin{array}{rl}\frac{\sin x}{x}& =1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\frac{x^8}{9!}-\frac{x^{10}}{11!}+\cdots \\ & =(1-\frac{x^2}{{\pi }^2})(1-\frac{x^2}{2^2{\pi }^2})(1-\frac{x^2}{3^2{\pi }^2})\cdots \end{array}$$

Because two polynomials are the same if and only if the coefficients of all their terms are equal, Euler attempts to generalize this to infinite expressions, and equate the coefficients for $\sin$. The constant coefficient is easy - we can read it off as $1$ from both the series and the product, but the quadratic term already holds a deep and surprising truth.

From the series, we can again simply read off the coefficient as $-1/3!$. But from the product, we need to think - after multiplying everything out, what sort of products will lead to a term with $x^2$? Since each factor is already quadratic this is more straightforward than it sounds at first - the only way to get a quadratic term is to take one of the quadratic terms already present in a factor, and multiply it by 1 from another factor! Thus, the quadratic terms are $-\frac{x^2}{2^2{\pi }^2}-\frac{x^2}{3^2{\pi }^2}-\frac{x^2}{4^2{\pi }^2}-\cdots$. Setting the two coefficients equal (and dividing out the negative from each side) yields

$$\frac{1}{3!}=\frac{1}{{\pi }^2}+\frac{1}{2^2{\pi }^2}+\frac{1}{3^2{\pi }^2}+\cdots$$

Which quickly leads to a solution to the original problem, after multiplying by ${\pi }^2$:

$$\frac{{\pi }^2}{3!}=1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots$$

Euler had done it! There are of course many dubious steps taken along the way in this argument, but calculating the numerical value,

$$\frac{{\pi }^2}{3!}=1.64493406685\dots$$

We find it to be exactly the number the series is heading towards. This gave Euler the confidence to publish, and the rest is history.

But we analysis students should be looking for potential troubles in this argument. What are some that you see?

Viète’s Infinite Trigonometric Identity

Viete was a French mathematician in the mid 1500s, who wrote down for the first time in Europe, an exact expression for $\pi$ in 1596.

Proposition 8 (Viète’s formula for $\pi$) $$\frac{2}{\pi }=\frac{\sqrt{2}}{2}\frac{\sqrt{2+\sqrt{2}}}{2}\frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}\frac{\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}{2}\cdots$$

Viete’s original publicaiton of this formula - it predates our modern notation for square roots!

How could one derive such an incredible looking expression? One approach uses trigonometric identities…an infinite number of times! Start with the familiar function $\sin (x)$. Then we may apply the double angle identity to rewrite this as

$$\sin (x)=2\sin \left(\frac{x}{2}\right)\cos \left(\frac{x}{2}\right)$$

Now we may apply the double angle identity once again to the term $\sin (x/2)$ to get

$$\begin{array}{rl}\sin (x)& =2\sin \left(\frac{x}{2}\right)\cos \left(\frac{x}{2}\right)\\ & =4\sin \left(\frac{x}{4}\right)\cos \left(\frac{x}{4}\right)\cos \left(\frac{x}{2}\right)\end{array}$$

and again

$$\sin (x)=8\sin \left(\frac{x}{8}\right)\cos \left(\frac{x}{8}\right)\cos \left(\frac{x}{4}\right)\cos \left(\frac{x}{2}\right)$$

and again

$$\sin (x)=16\sin \left(\frac{x}{16}\right)\cos \left(\frac{x}{16}\right)\cos \left(\frac{x}{8}\right)\cos \left(\frac{x}{4}\right)\cos \left(\frac{x}{2}\right)$$

And so on….after the $n^{th}$ stage of this process one can re-arrange the the above into the following (completely legitimate) identity:

$$\frac{\sin x}{2^n\sin \frac{x}{2^n}}=\cos \frac{x}{2}\cos \frac{x}{4}\cos \frac{x}{8}\cos \frac{x}{16}\cdots \cos \frac{x}{2^n}$$

Viete realized that as $n$ gets really large, the function $2^n\sin (x/2^n)$ starts to look a lot like the function $x$…and making this replacement in the formula as we let $n$ go to infinity yields

Proposition 9 (Viète’s Trigonometric Identity) $$\frac{\sin x}{x}=\cos \frac{x}{2}\cos \frac{x}{4}\cos \frac{x}{8}\cos \frac{x}{16}\cdots$$

An incredible, infinite trigonometric identity! Of course, there’s a huge question about its derivation: are we absolutely sure we are justified in making the denominator there equal to $x$? But carrying on without fear, we may attempt to plug in $x=\pi /2$ to both sides, yielding

$$\frac{2}{\pi }=\cos \frac{\pi }{4}\cos \frac{\pi }{8}\cos \frac{\pi }{16}\cos \frac{\pi }{32}\cdots$$

Now, we are left just to simplify the right hand side into something computable, using more trigonometric identities! We know $\cos \pi /4$ is $\frac{\sqrt{2}}{2}$, and we can evaluate the other terms iteratively using the half angle identity:

$$\cos \frac{\pi }{8}=\sqrt{\frac{1+\cos \frac{\pi }{4}}{2}}=\sqrt{\frac{1+\frac{\sqrt{2}}{2}}{2}}=\frac{\sqrt{2+\sqrt{2}}}{2}$$

$$\cos \frac{\pi }{16}=\sqrt{\frac{1+\cos \frac{\pi }{8}}{2}}=\sqrt{\frac{1+\frac{\sqrt{2+\sqrt{2}}}{2}}{2}}=\frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}$$

Substituting these all in gives the original product. And, while this derivation has a rather dubious step in it, the end result seems to be correct! Computing the first ten terms of this product on a computer yields $0.63662077105\dots$, wheras $2/\pi =0.636619772$. In fact, Viete used his own formula to compute an approximation of $\pi$ to nine correct decimal digits. This leaves the obvious question, Why does this argument work?

The Infinitesimal Calculus

In trying to formalize many of the above arguments, mathematicians needed to put the calculus steps on a firm footing. And this comes with a whole collection of its own issues. Arguments trying to explain in clear terms what a derivative or integral was really supposed to be often led to nonsensical steps, that cast doubt on the entire procedure. Indeed, the history of calculus is itself so full of confusion that it alone is often taken as the motivation to develop a rigorous study of analysis. Because we have already seen so many other troubles that come from the infinite, we will content ourselves with just one example here: what is a derivative?

The derivative is meant to measure the slope of the tangent line to a function. In words, this is not hard to describe. But like the sine function, this does not provide a means of computing, and we are looking for a formula. Approximate formulas are not hard to create: if $f(x)$ is our function, and $h$ is some small number the quantity

$$\frac{f(x+h)-f(x)}{h}$$

represents the slope of the secant line to $f$ between $x$ and $h$. For any finite size in $h$ this is only an approximation, and so thinking of this like Archimedes did his polygons and the circle, we may decide to write down a sequence of ever better approximations:

$$D_n=\frac{f(x+\frac{1}{n})-f(x)}{\frac{1}{n}}$$

and then define the derivative as the infiniteth term in this sequence. But this is just incoherent, taken at face value. If $1/n\to 0$ as $n\to \mathrm{\infty }$ this would lead us to

$$\frac{f(x+0)-f(x)}{0}=\frac{0}{0}$$

So, something else must be going on. One way out of this would be if our sequence of approximates did not actually converge to zero - maybe there were infinitely small nonzero numbers out there waiting to be discovered. Such hypothetical numbers were called infinitesimals.

Definition 6 (Infinitesimal) A positive number $\epsilon$ is infinitesimal if it is smaller than $1/n$ for all $n\in \mathbb{N}$.

This would resolve the problem as follows: if $dx$ is some infinitesimal number, we could define the derivative as

$$D=\frac{f(x+dx)-f(x)}{dx}$$

But this leads to its own set of difficulties: its easy to see that if $\epsilon$ is an infinitesimal, then so is $2\epsilon$, or $k\epsilon$ for any rational number $k$.

Exercise 13 Prove this: if $\epsilon$ is infinitesimal and $k\in \mathbb{Q}$ show $k\epsilon$ is infinitesimal$.

So we can’t just say define the derivative by saying “choose some infinitesimal $dx$” - there are many such infinitesimals and we should be worried about which one we pick! What actually happens if we try this calculation in practice, showcases this.

Let’s attempt to differentiate $x^2$, using some infinitesimal $dx$. We get

$$(x^2{)}^{\prime }=\frac{(x+dx{)}^2-x^2}{dx}=\frac{x^2+2xdx+d{x}^2-x^2}{dx}$$ $$=\frac{2xdx+d{x}^2}{dx}=2x+dx$$

Here we see the derivative is not what we expected, but rather is $2x$ plus an infinitesimal! How do we get rid of this? One approach (used very often in the foundational works of calculus) is simply to discard any infinitesimal that remains at the end of a computation. So here, because $2x$ is finite in size and $dx$ is infinitesimal, we would just discard the $dx$ and get $(x^2{)}^{\prime }=2x$ as desired.

But this is not very sensible: when exactly are we allowed to do this? If we can discard an infinitesimal whenever its added to a finite number, shouldn’t we already have done so with the $(x+dx)$ that showed up in the numerator? This would have led to

$$\frac{(x+dx{)}^2-x^2}{dx}=\frac{x^2-x^2}{dx}=\frac{0}{dx}=0$$

So, the when we throw away the infinitesimal matters deeply to the answer we get! This does not seem right. How can we fix this? One approach that was suggested was to say that we cannot throw away infinitesimals, but that the square of an infinitesimal is so small that it is precisely zero: that way, we keep every infinitesimal but discard any higher powers. A number satisfying this property was called nilpotent as nil was another word for zero, and potency was an old term for powers ($x^2$ would be the *second potency of $x$).

Definition 7 A number $\epsilon$ is nilpotent if $\epsilon \ne 0$ but ${\epsilon }^2=0$.

If our infinitesimals were nilpotent, that would solve the problem we ran into above. Now, the calculation for the derivative of $x^2$ would proceed as

$$\frac{(x+dx{)}^2-x^2}{dx}=\frac{x^2+2xdx+d{x}^2-x^2}{=}\frac{2xdx+0}{dx}=2x$$

But, in trying to justify just this one calculation we’ve had to invent two new types of numbers that had never occurred previously in math: we need positive numbers smaller than any rational, and we also need them (or at least some of those numbers) to square to precisely zero. Do such numbers exist?